La dinámica compleja estudia el comportamiento de funciones holomorfas $$f$$ definidas en alguna superficie de Riemann $$S$$. Un caso clásico es cuando $$S=\mathbb{C}$$ y $$f$$ es un polinomio cuadrático, que sin perder generalidad se puede escribir como $$f_c(z) := z^2 + c$$ para algún $$c\in \mathbb{C}$$. Dado $$x_0\in \mathbb{C}$$, podemos preguntar si es que la órbita $$\{f_c^{\circ n}(x_0)\}_{n\geq 0}$$ escapa o no a infinito, y a qué velocidad lo hace. Un teorema, el llamado Criterio de Escape, indica que si alguno de estos iterados tiene valor absoluto mayor que cierto threshold, entonces la órbita efectivamente se dispara a infinito.

Un método gráfico estándar es para cada $$x_0\in \mathbb{C}$$, y para cada iterado de $$f_c(x_0)$$ verificar si su valor absoluto excede dicho threshold. De hacerlo, se colorea $$x_0$$ blanco, y de lo contrario, negro. La parte negra se llama el conjunto de Julia lleno de $$f$$, denotado $$\mathcal{K}_c$$. Una implementación rudimentaria con $$c=0.285 - 0.01i$$ de este método lleva a la siguiente imagen aproximada de $$\mathcal{K}_c$$:

Esto nos permite visualizar qué puntos son atrapados en la órbita de $$f_c$$. Para poder ver la velocidad de escape, coloreamos de acuerdo a cuántas iteraciones el Criterio de Escape falla. Más explícitamente, a priori fijamos un $$N\in\mathbb{N}$$, nuestra tolerancia para el número de iteraciones. Si en algún momento hemos iterado sobre un mismo $$x_0$$ más de $$N$$ veces, o el valor absoluto de un iterado es mayor al radio de escape, dicho $$x_0$$ escapa y se le asigna el entero $$N$$; si la órbita escapa antes de llegar a $$N$$ iterados, le asignamos la cantidad de iterados que le tomó en escapar. Así, para cada $$x_0\in \mathbb{C}$$ tenemos un número entre $$0$$ y $$N$$ que lleva cuenta de cuánto demora un punto en escapar (relativo a $$N$$), que podemos normalizar (dividiendo por $$N$$), y por lo tanto asignar un bitmap. El mismo $$\mathcal{K}_c$$ anterior coloreado de acuerdo a este método (con el bitmap turbo de matplotlib) resulta en:

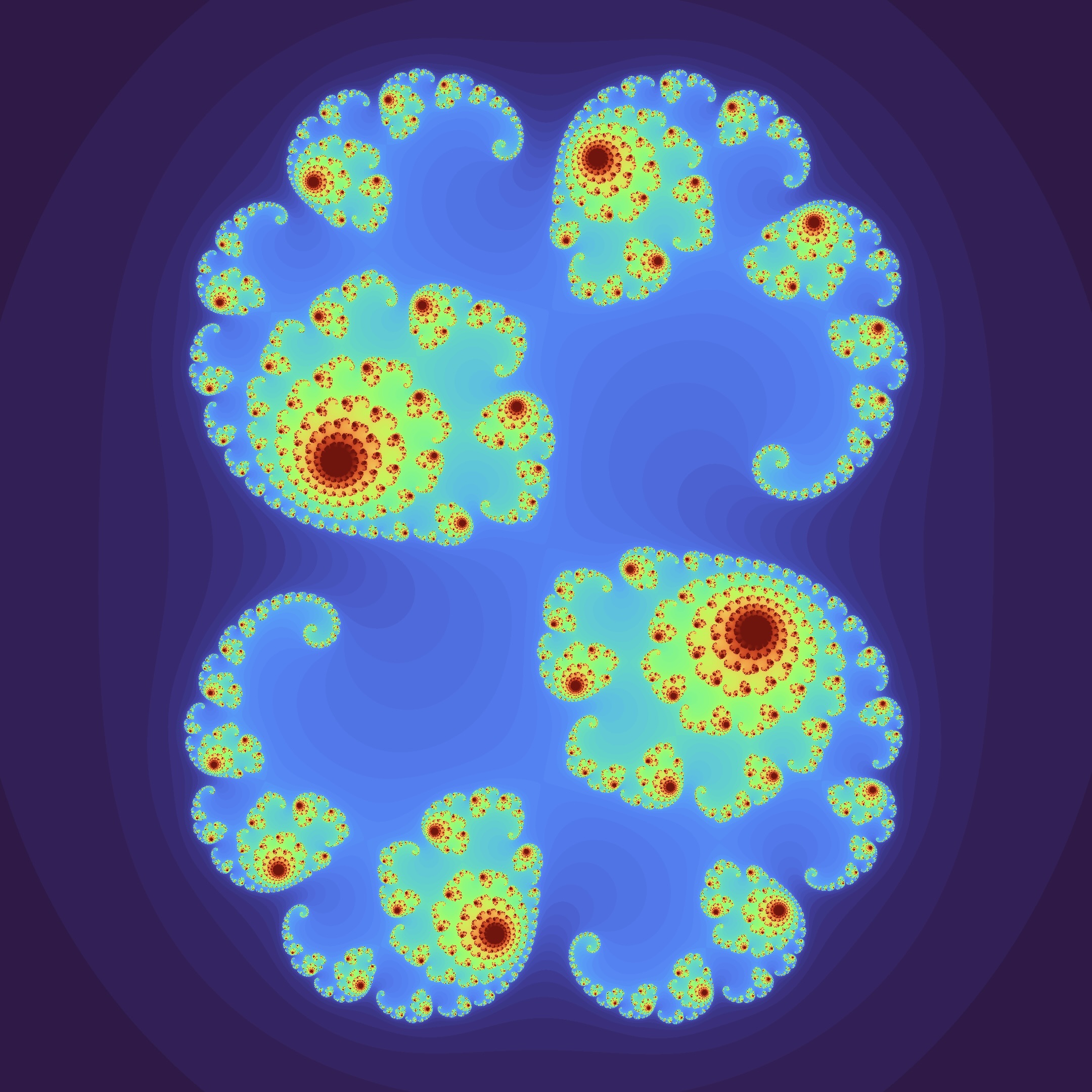
En la figura, mientras más cálido el color, más lento escapa la órbita de $$f_c$$ en tal punto. A simple vista es evidente la autosimilitud de $$\mathcal{K}_c$$, y la presencia de regiones muy calientes, en cuyo corazón se encuentran los llamados puntos atractores, que terminarán por abosrber todas las órbitas que pasen suficientemente cerca de el.